La derivación logarítmica es una técnica de derivación que nos permite hallar la derivada de una función aplicando las propiedades de los logaritmos. Aunque se puede utilizar para resolver muchos tipos de derivadas, es especialmente útil para las funciones de tipo potencial-exponencial: f x = g x ϕ x. Como ves, f (x) es una función g (x.. Aquí encontrarás cómo resolver la derivada de una función logarítmica en cualquier base (fórmula). Además, podrás practicar con ejercicios resueltos paso a paso de derivadas de funciones logarítmicas. La fórmula para dividir una función logarítmica depende de si el logaritmo es natural (de base e) o de cualquier otra base.

Integrales de funciones logarítmicas y exponenciales Derivadas

Las Derivadas de Funciones Logarítmicas y exponenciales Cálculo Diferencial CiberTareas

Derivada de la función exponencial Ejemplo 2 YouTube

DERIVADAS DE FUNCIONES LOGARITMICAS YouTube

Derivadas de funciones logarítmicas y exponenciales. Bachillerato. YouTube
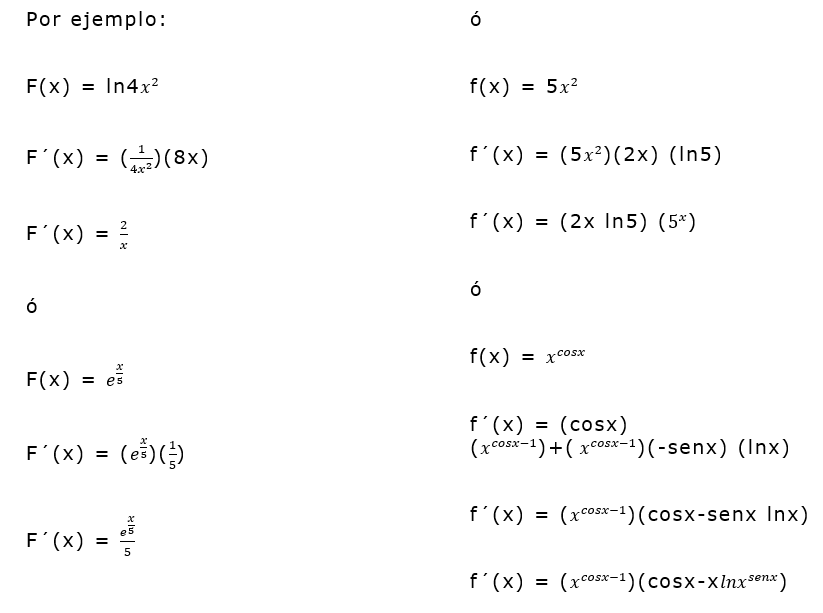
Adictos al Cálculo Derivadas de funciones exponenciales y logarítmicas

Derivada de una función exponencial Qué es, definición y concepto
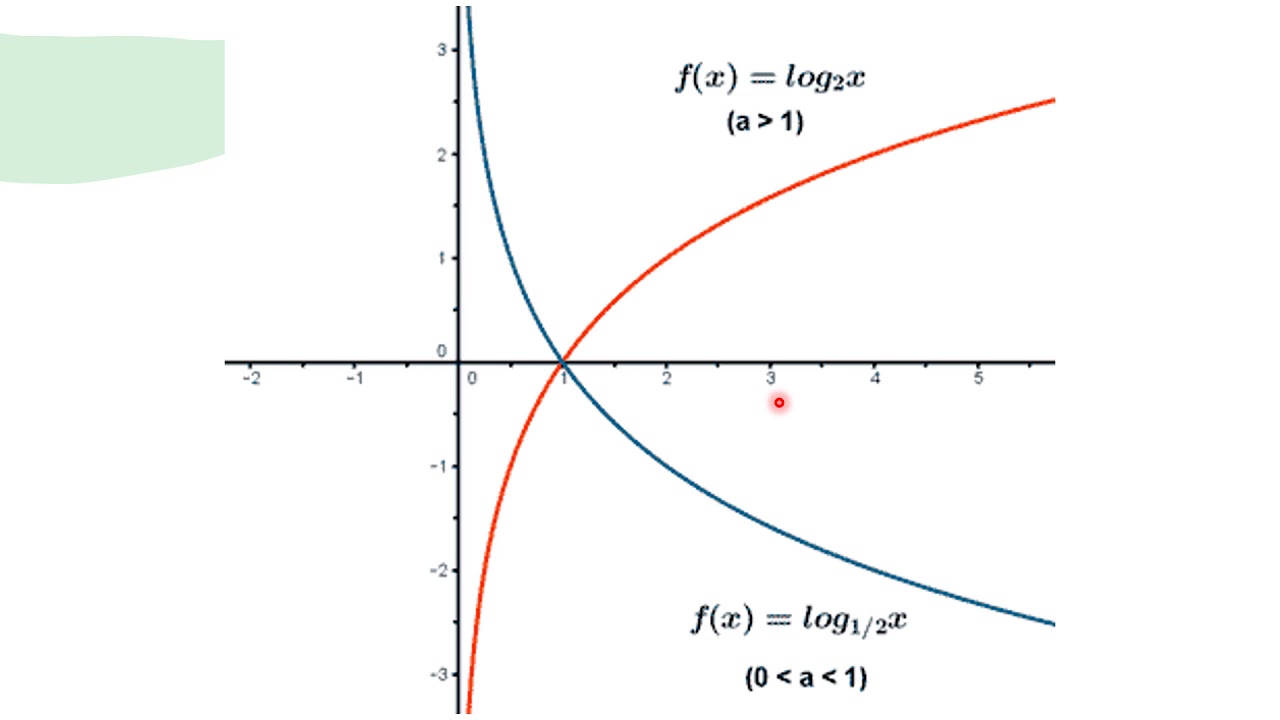
Funciones exponenciales y logarítmicas YouTube

DERIVADAS de FUNCIONES EXPONENCIALES y LOGARITMICAS ejercicios resueltos 001 💣💥💡 RAPIDO Y FACIL
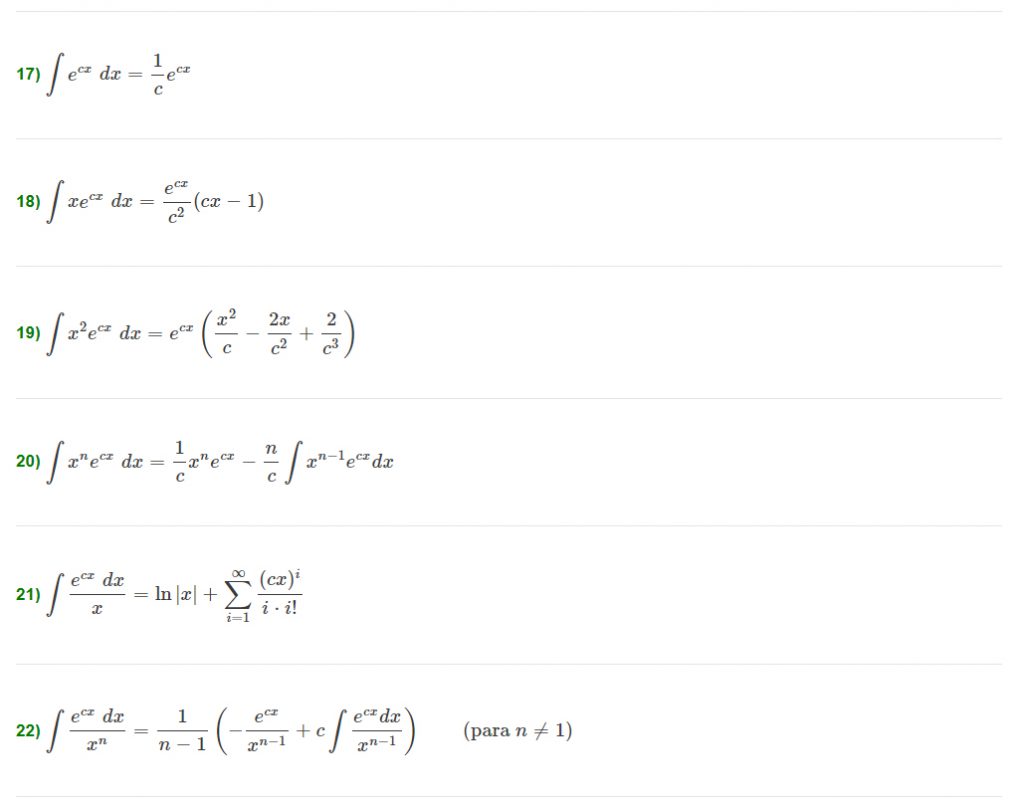
Integrales de funciones logarítmicas y exponenciales Derivadas

» Derivada de polinomios y funciones exponenciales Ejercicios Resueltos

Derivadas 2 Función Exponencial MCC YouTube

Derivadas tipo logarítmicas YouTube

Derivadas de funciones exponenciales y logarítmicas. Fórmulas matematicas. Geometría, física

Derivada de funciones exponenciales y logarítmicas YouTube

Integrales de funciones logarítmicas y exponenciales Derivadas

Funciones exponenciales y logarítmicas YouTube

5 funciones logaritmicas y exponenciales

DERIVADA DE LA FUNCIÓN LOGARÍTMICA YouTube

Integrales de funciones logarítmicas y exponenciales Derivadas
This page titled 3.9: Derivadas de funciones exponenciales y logarítmicas is shared under a CC BY-NC-SA 4.0 license and was authored, remixed, and/or curated by Edwin “Jed” Herman & Gilbert Strang via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.. Para comenzar, intentaremos adivinar C(a), algunos valores de a, enchufando algunos valores pequeños de h. Ejemplo 2.7.1 Estimaciones de C(a). Vamos a = 1 entonces C(1) = lim h → 0 1h − 1 h = 0. Esto no es sorprendente ya que 1x = 1 es constante, y así su derivada debe ser cero en todas partes.

